How to plot the graph of the reciprocal of a function ?
Given the function y = F(x), the question is how to define and plot the graph of G(x) = 1/ F(x).
A number of simple rules listed below describe how the graph characteristics of F (extrema, asymptotes, X-intercept points) are transformed in the graph of 1/F.
In addition, the following applies:
- Point-by-point correspondence: if (x,y) is a point of F(x), then (x, 1/y) is the corresponding point of G(x),
- If F(x) is increasing in a given interval of x, then G(x) = 1/F(x) is decreasing in the same interval,
- Vice-versa: if F(x) is decreasing in a given interval of x, then G(x) = 1/F(x) is increasing in the same interval.
Rule 1: Transformation of extrema
- If (a,b) is a maximum of F(x) , then (a,1/b) is a minimum of G(x),
- If (a,b) is a minimum of F(x) , then (a,1/b) is a maximum of G(x).
Rule 2: Horizontal asymptotes
A horizontal asymptote of F(x) e.g. y = b becomes a horizontal asymptote y = 1/b of G(x).
In other words:
- If Limit of F(x) when x goes to -∞ is b, then: Limit of G(x) when x goes to -∞ is 1/b,
- If Limit of F(x) when x goes to +∞ is b, then: Limit of G(x) when x goes to +∞ is 1/b .
Rule 3: Vertical asymptotes
A vertical asymptote x = a of F(x) becomes a x-intersect point (a, 0) of G(x).
In other words: If Limit of F(x) when x goes to a is +∞ or -∞, then: G(a) = 0 .
Rule 4: X-intersect points - this is the reciprocal of rule 3 -
A x-intersect point of F(x) for instance a such that F(a) = 0 becomes a vertical asymptote x = a of G(x).
In other words:
- If F(a) = 0 and F is increasing at point a, then:
- Limit of G(x) when x goes to a- is -∞
- Limit of G(x) when x goes to a+ is +∞
- If F(a) = 0 and F is decreasing at point a, then:
- Limit of G(x) when x goes to a- is +∞
- Limit of G(x) when x goes to a+ is -∞
Example
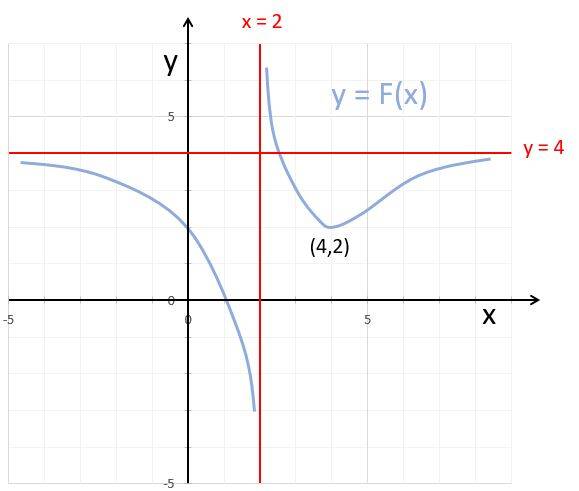
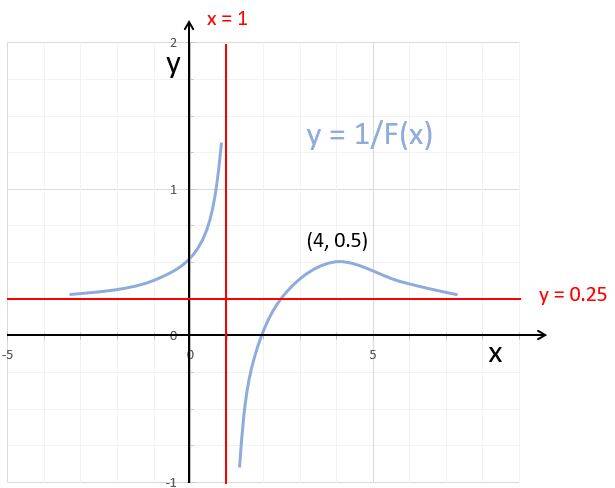
F(x) and 1/F(x) graphs characteristics:
- Transformation of extrema: (4,2) minimum of F ⇒ (4, 0.5) maximum of 1/F
- Horizontal asymptote: Horizontal asymptote of F: y = 4 ⇒ horizontal asymptote of 1/F: y = 0.25
- Vertical asymptote: Vertical asymptote of F: x = 2 ⇒ x-intersect point of 1/F: (2. 0)
- X-intersect point: X-intersect point of F (1, 0) ⇒ vertical asymptote of 1/F: x = 1
Maak jouw eigen website met JouwWeb