INTEGRATION AND PRIMITIVE ESSENTIALS
INTRODUCTION
Integrals together with derivatives are fundamental objects in Calculus; a very clear conceptual understanding of these is a must. This chapter summarizes the principles of integration and the link between integrals and primitives.
DEFINITE INTEGRAL - DEFINITION
Let f denote a continuous and positive function on an interval [a, b].
By definition the Definite Integral of f between a and b, denoted by ∫ab f or ∫ab f(t)dt, is the area between the f curve and the abscissa axis, delimited by a and b.
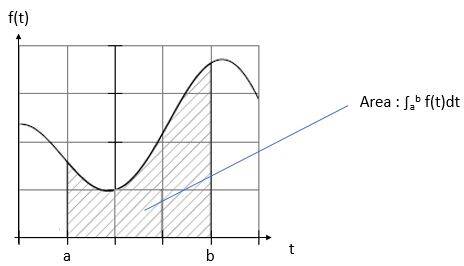
It is called a “definite” integral because of its dependence on the two given constants a and b.
The concept can be extended to a non-positive function, bearing in mind that areas in the negative portions of the function are negative.
INDEFINITE INTEGRAL or PRIMITIVE
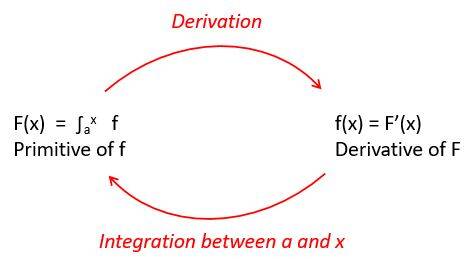
The Indefinite Integral or Primitive is a generalization of the Definite Integral. It is a function (as opposed to a definite value) depending on a variable, say x, which replaces the constant value b.
Notation: F(x) = ∫ax f also written as ∫ax f(t)dt
KEY PROPERTIES OF PRIMITIVES
- F’(x) = f(x): given that F(x) = ∫ax f , then the derivative of F is f ; the primitive can be looked at as the “inverse” of the derivative.
- If F is a primitive of f then F plus any constant is also a primitive of f, since the derivative of a constant is 0; so there is an infinite number of primitives of a given function f, all differing by a constant term.
- ∫ab f = F(b) – F(a): formula to calculate a Definite Integral as the difference of the primitive at two given points b and a.
IN SUMMARY
EXAMPLE APPLICATIONS
- Direct calculation of ∫ab f for a given function f
∫ab f = F(b) – F(a) where F is the primitive of f .
It is then just a matter of identifying F given the function f, based on the knowledge of derivatives of common functions provided one of them is applicable.
Simple example:
f(x) = x ; find ∫ab f = ∫ab x
Derivative of x2 is 2x and derivative of x2/2 is x
Therefore the primitive de f(x) is F(x) = x2/2 and ∫ab f = b2/2 – a2/2
- INTEGRATION BY PARTS: a useful technique for finding the integral of a function when expressed as a product uv’ where v’ is a derivative of which we know the primitive.
Formula: ∫ uv’= uv - ∫ u’v
Example 1: ∫ x cos(x)
u = x ; v’ = cos(x)
u’ = 1 ; v = sin(x)
⇒ ∫ x cos(x) = x sin(x) - ∫ sin(x) = x sin(x) + cos(x) + constant
Example 2: ∫ x ln(x)
u = ln(x) ; v’ = x
u’ = 1/x ; v = x2/2
⇒ ∫ x ln(x) = x2 ln(x)/2 - ∫(1/x) (x2/2) = x2 ln(x)/2 - ∫ x/2 = x2 ln(x)/2 - x2/4 + constant
- INTEGRATION BY SUBSTITUTION: a useful technique for finding the integral of a function when expressed as a product of a composite function g ∘ f (x) = g [f(x)] and of the derivative of f.
Formula: ∫ g [ f(x)] f’(x) dx = ∫ g(y) dy
after substituting f(x) for y and f’(x) dx for dy.
Example: ∫ sin(√x) / √x dx
y = √x
dy = 1 / 2√x dx
⇒ ∫ sin(√x) / √x dx = ∫ sin(y) * (2 dy) = 2 ∫ sin(y) dy = -2 cos(y) = -2 cos(√x) + constant
Maak jouw eigen website met JouwWeb