Trigonometry Primer

1. Introduction

Trigonometry is everywhere and used in many branches of science and technology: geography, astronomy, electrical engineering, architecture, etc…

The basic concepts are presented here, mostly in pictures and a few formulas. Also, there is a short test at the end !

2. Unit of measure of angles

Two types of units are used for angles: radians and degrees. This is important to master fully and be able to easily go from one set of units to the other.

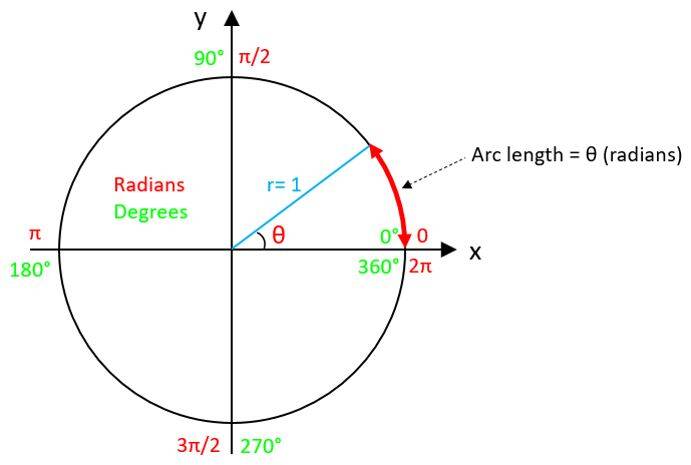
Angle θ in radians = length of the arc intercepted by the angle θ on the unit circle.

θ = 2π that corresponds to one full rotation on the unit circle, is the perimeter of the unit circle of radius of 1 (Perimeter = 2 π * Radius).

π/2 radians ➜ 90⁰

π radians ➜ 180⁰
2π radians ➜ 360⁰

3. Sinus and cosinus formulas

Considering the rectangle triangle below:

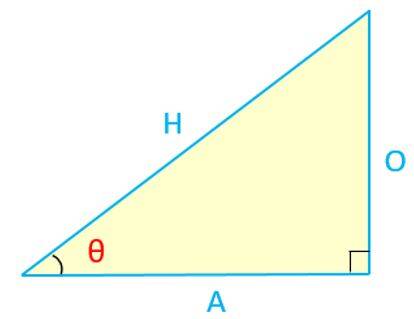
Sinus, cosinus and tangent formulas:

Sin(θ) = O / H = Opposite / Hypotenuse
Cos(θ) = A / H = Adjacent / Hypotenuse
Tg(θ) = O / A = Opposite / Adjacent

Helpful mnemonic: SOH-CAH-TOA

4. Trigonometric circle

The trigonometric circle is an important tool to work with angles, for a clear understanding of the relationship to the trigonometric functions and periodicity:

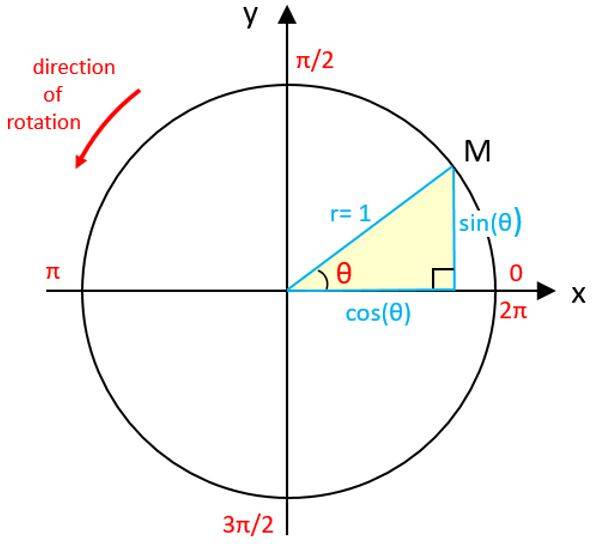
Notes:

Point M coordinates: x = cos(θ), y = sin(θ)
Equation of the unit cercle: x² + y² = 1
Special case of Pythagora: sin²(θ) + cos²(θ) = 1

5. Trigonometric circle and Sinus function

How the trigonometric circle relates to the Sinus function graph:

There is a similar figure for cosinus; compared to the sinus curve, cosinus is shifted by π/2 to the left.

6. Test yourself

Can you identify the following trigonometric functions curves ?

Solution:

Curve 1: - sin(x)

Curve 2: cos(x-π/4)

Curve 3: 1.5 cos(x/2)